Tutor
Welcome to MAT 130. Linear Algebra.
Determinant of a Matrix:
2 by 2 matrix:
3 by 3 Matrix:
NxN Matrix:
Before proceeding to the calculation of the determinant of an NxN matrix, you have to learn about some concepts such as the Minors and the Cofactors. Please have a look at the following link:
http://www.utdallas.edu/dept/abp/PDF_Files/LinearAlgebra_Folder/Cofactors.pdf
Do not pay a great attention to the section where we are talking about the adjoint and the Inverse, we will discuss this stuff later on.
Please have a look at the following Video:
PS/ The Cofactor Expansion provides a method for taking the determinant of a matrix which is fairly useful when computations are being done manually.
Tricks:
You have always to expand by the row or column that contain the highest number of zeros
If a is a triangular matrix then detA is the product of the entries on the main diagonal.
if you didn't get it, please review the video above, it covers all these points.
Homework: P 182 EX 1-----10 + 18 + 19 + 20 + 26.
Section 4.2: Properties of Determinants
Intresting Links: http://www.wiziq.com/tutorial/8083-properties-of-Determinants
http://tutorial.math.lamar.edu/Classes/LinAlg/DeterminantProperties.aspx
You can also have a look at the word file bellow; It's pertty much intesting and well presented. Hope you get full advantage of it.

|
MAT 130 PROPERTIES OD DETERMINANTS.doc Size : 127 Kb Type : doc |
Row operations for determinants
Homework: EX 1----7 Page; 192
Section 4.3: Cramer's Rule; Formula for the inverse of A ; Applications of determinants
Adjoint
The matrix formed by taking the transpose of the cofactor matrix of a given original matrix. The adjoint of matrix A is often written adj A.
Note: This is in fact only one type of adjoint. More generally, an adjoint of a matrix is any mapping of a matrix which possesses certain properties. Consult a book on linear algebra for more information.
| Example: | Find the adjoint of the following matrix:
|
| Solution: | First find the cofactor of each element.
As a result the cofactor matrix of A is
Finally the adjoint of A is the transpose of the cofactor matrix:
|
.
Adjoint method for finding the inverse: A-1 = |
Example: The following steps result in A-1 for The cofactor matrix for A is
|
Solving a 3 X 3 Linear System using Cramer's Rule:
Diagonalization : " Eigenvalues and Eigenvectors "
Please Study these Links:
http://sosmath.com/matrix/eigen2/eigen2.html
Differential Equations:
Introduction to differential equations:
Separable differential equations:
Second example:
If You prefer handouts, please try the following links:
http://www-math.mit.edu/~djk/18_01/chapter15/contents.html
Lagrange Multipliers
Lagrange Multiplier.
A second lecture
A third well structured lecture.
In this thrid video, the lecturer focused only on explaining the lagrange methode as a whole and independent concept. He did not talk about maximum or minimum.
if you want to learn more about maximum and minimum, please have a look at the two videos above.
Real world example. #1.
Real world example. #2.
![\[{\rm{A}} = \left[ {\begin{array}{*{20}c} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 1 & 0 & 6 \\\end{array}} \right]\]](http://www.mathwords.com/a/a_assets/adjoint1.gif)

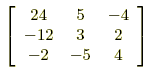

 .
. , so the adjoint is
, so the adjoint is 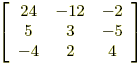 . Since
. Since  .
.